Physics 237, Midterm Exam #2
Thursday
March 25, 2010
12.30
pm – 1.45 pm
Do not
turn the pages of the exam until you are instructed to do so.
Exam
rules: You may use only a writing instrument while taking
this test. You may not consult any calculators, computers,
books, or each other.
1. Problems 1 and 2 must be answered in booklet # 1.
2. Problems 3 and 4 must be answered in booklet # 2.
3. The answers need to be well motivated and expressed in terms of the variables used in the problem. You will receive partial credit where appropriate, but only when we can read your solution. Answers that are not motivated will not receive any credit, even if correct.
At the end of the exam, you need to hand
in your exam, your Ņcheat sheetÓ, and the two blue exam booklets. All items must be clearly labeled with
your name, your student ID number, and the day/time of your workshop.
Name:
__________________________________________________
ID number:
______________________________________________
Workshop
Day/Time: ______________________________________
Problem 1 (30 points) ANSWER
IN BOOKLET 1
A particle of mass m and energy 
is
approaching x = 0 from the left. The potential seen by the particle can
be described by the following function:
a)
What is the wave
function in the region x < 0? You can set the amplitude of the
incident wave to 1.
b)
What is the wave
function in the region x ³ 0?
c)
Calculate the
transmission coefficient.
Your answers need to be well
motivated. A correct answer
without any motivation will not receive any credit.
Problem 2 (30 points) ANSWER
IN BOOKLET 1
Consider a particle of mass m,
located in a region where the potential V
is given by
a)
Show that 
can be an eigenfunction
describing this system.
b)
What is the value of α?
c)
What is the value of A?
d)
What is the energy E for this eigenfunction?
e)
What is the expectation value of x?
f)
What is the expectation value of x2?
Your answers need to be well
motivated. A correct answer
without any motivation will not receive any credit.
Problem 3 (35 points) ANSWER
IN BOOKLET 2
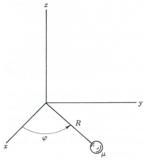A particle of mass m is fixed at one end of a rigid rod of negligible mass and length R, as shown in the Figure. The other end of the rod rotates in the
x-y plane about a bearing located at
the origin, whose axis is in the z
direction. The Schrdinger
equation for this system is
where 
is the
moment of inertia of the mass with respect to the z axis and 
is the
wavefunction.
a)
Assuming that
the wavefunction can be written as
show that
the angle-dependent part of the wavefunction must satisfy the following
time-independent Schrdinger equation:
where E is the total energy.
b)
Show that
is a
solution of the time-independent Schrdinger equation.
c)
Since the system
should not change when the azimuthal angle changes by 2¹, what constraint does this impose on the possible values of m?
d)
Find the
selection rule for transitions between the energy states of this rigid rotor,
assuming that the mass carries a charge –e.
Your answers need to be well
motivated. A correct answer
without any motivation will not receive any credit.
Problem 4 (5 points) ANSWER
IN BOOKLET 2
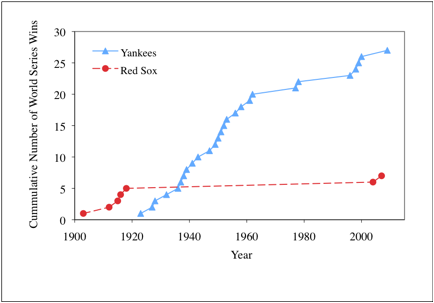
The following graph shows the
cumulative World Series wins of the Yankees and the Red Sox, as function of
year. After careful examination of
these scientific data, which is the better team?
1. The Yankees.
2. The Red Sox.
3. The Buffalo Bills.
4. I do not know.