Write the following text on the front cover of your homework
assignment and sign it. If the text is missing, 20 points will be subtracted
from your homework grade.

1.
Show
that none of the principal moments of inertia can exceed the sum of the other
two.
2.
A
uniform rod of length b stands
vertically upright on a rough floor and then tips over. What is the rod's angular velocity when
it hits the floor?
3.
Find
the frequency of small oscillations for a thin homogeneous plate if the motion
takes place in the plane of the plate and if the plate has the shape of an
equilateral triangle and is suspended
(a)
from
the midpoint of one side.
(b)
from one apex.
4.
A
physical or compound pendulum is a rigid body that oscillates due to its own
weight about a horizontal axis that does not pass through the center of mass of
the body (see Figure).
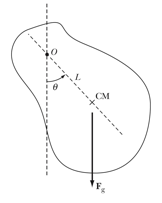
Assume the pendulum of mass M is released from rest from an angle q0. Determine the
angular velocity w as function of the angle q. Note: do not assume that the angles are
small.
This set covers the material discussed in Chapter 11.