Write the following text on the front cover of your homework assignment and
sign it. If the text is missing, 20 points will be subtracted from your
homework grade.

1. A double pendulum consists of two simple pendula, with one pendulum suspended from the bob of the other. If the two pendula have equal lengths, have bobs of equal mass, and are confined to move in the same plane, find Lagrange's equations of motion for the system. Do not assume small angles.
2. A particle of mass m can slide freely along a wire AB whose perpendicular distance to the origin O is h (see Figure below).
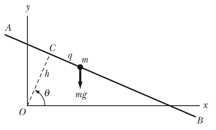
The line OC rotates about the origin at a constant rate dq/dt = w. The position of the particle can be described in terms of the angle q and the distance q to the point C. If the particle is subject to a gravitational force, and if the initial conditions are
![]()
show that the time dependence of the coordinate q is
![]()
Sketch the result. Compute the Hamiltonian for the system, and compare it with the total energy. Is the total energy conserved?
3. Two masses m1 and m2 (m1 ≠ m2) are connected by a rigid rod of length d and of negligible mass. An extensionless string of length l1 is attached to m1 and connected to a fixed point of support P. Similarly, a string l2 (l1 ≠ l2) connects m2 to P. Obtain the equation describing the motion of this system in the plane of m1, m2, and P, and find the frequency of small oscillations around the equilibrium position.
4. A particle is constrained to move (without friction) on a circular wire rotating with a constant angular speed w about a vertical diameter. Find the equilibrium position of the particle, and calculate the frequency of small oscillations around this position. Find and interpret physically a critical angular velocity w = wc that divides the particle's motion into two distinct types. Construct a phase diagram for the two cases w < wc and w > wc.
5. A particle of mass m moves under the influence of gravity along the helix z = kq, r = constant, where k is a constant and z is the coordinate along the vertical axis. Obtain the Hamiltonian equations of motion.
This set covers the material discussed in Chapter 7.