Physics 235, Final Exam
December 18, 2018: 12.30 pm – 3.30 pm
Do not turn the pages of the exam until you are instructed to do so.
Exam rules: You may use only a writing instrument while taking this test. You may not consult any calculators, computers, books, call phones, nor each other.
The answers need to be well motivated and expressed in terms of the variables used in the problem. You will receive partial credit where appropriate, but only when we can read your solution. Answers that are not motivated will not receive any credit, even if correct.
At the end of the exam, you need to hand in your exam, the blue exam booklets, and the equation sheet. All items must be clearly labeled with your name, your student ID number, and the day/time of your recitation. If any of these items are missing, we will not grade your exam, and you will receive a score of 0 points.
Answer questions 1 - 3 in exam book 1, questions 4 – 6 in exam book 2, and questions 7 - 9 in exam book 3.
You are required to complete the following Honor Pledge for Exams. Copy and sign the pledge before starting your exam.
“I affirm that I will not give or receive any unauthorized help on this exam, and that all work will be my own.”
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Name: ______________________________________________________________________
Signature: ____________________________________________________________________
Important instructions.
Read carefully.
1. There are 9 questions on this exam.
2. Question 9 (5 points) is a required question.
3. Questions 1 - 8 are each worth 15 points. You can skip one of these 8 questions. In the calculation of the final exam grade, I will drop the question with the lowest score (the question that you did not answer).
4. Based on this procedure, the maximum score you can receive on this exam will be 7x15 + 1x5 = 110 points.
5. The exam counts as a 100-point exam, so in principle, you can receive 10 extra points for this exam.

PROBLEM 1 (15 POINTS) ANSWER IN BOOK 1
Consider a rail road car moving with a constant acceleration a in the x direction. A simple pendulum of mass m and length L is placed inside the railroad car, as shown in the Figure below.
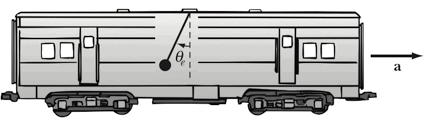
a) What is the Lagrangian of the pendulum?
b) What is the equation of motion of the angle q?
c) What is the equilibrium angle of the pendulum (qe)?
d) What is the frequency of small oscillations around the equilibrium angle?
Your answers must be well motivated and expressed in terms of the variables provided.
PROBLEM 2 (15 POINTS) ANSWER IN BOOK 1
Consider a “plucked string” of length L where the “plucked point” is a distance L/3 from one end, as shown in the Figure below. The density of the string is r and the tension in the string is t.
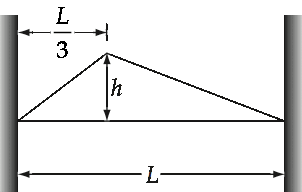
The string is released from rest in this configuration.
a) What are the initial conditions that must be satisfied by the displacement function q(x, t)?
b) What are the characteristic frequencies of the string?
c) Calculate the amplitude of the nth mode.
d) What is the displacement function q(x, t)?
Your answers must be well motivated and expressed in terms of the variables provided.
Useful relation:
![]()
PROBLEM 3 (15 POINTS) ANSWER IN BOOK 1
Three oscillators of equal mass m are coupled such that the potential energy of the system is given by
![]()
where
![]()
a) Find the eigen frequencies.
b) What are the physical interpretations of these eigen frequencies?
Your answers must be well motivated and expressed in terms of the variables provided.
PROBLEM 4 (15 POINTS) ANSWER IN BOOK 2
A particle of mass m starts at rest on top of a smooth fixed hemisphere of radius a.
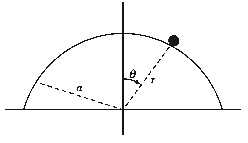
a) What is the equation of constraint?
b) What is the force of constraint?
c) At what angle will the particle leave the hemisphere?
Your answers must be well motivated and expressed in terms of the variables provided.
PROBLEM 5 (15 POINTS) ANSWER IN BOOK 2
Consider a simple plane pendulum consisting of a mass m attached to a string of length l. After the pendulum is set into motion, the length of the string is shortened at a constant rate:
![]()
The suspension point remains fixed.
a) Compute the Lagrangian.
b) Compute the Hamiltonian.
c) Compare the Hamiltonian and the total energy of the system, and discuss conservation of energy for this system.
Your answers must be well motivated and expressed in terms of the variables provided.
PROBLEM 6 (15 POINTS) ANSWER IN BOOK 2
A flexible cord of length L and mass M slides from a frictionless table top as shown in the Figure below.

The rope is released when a length y0 is hanging over the edge of the table.
a) What is the Lagrangian of this system when a length y is hanging over the edge of the table.
b) Use the Lagrangian to obtain the equation of motion.
c) At what time will the left end of the cord reach the edge of the table.
Your answers must be well motivated and expressed in terms of the variables provided.
PROBLEM 7 (15 POINTS) ANSWER IN BOOK 3
a) Consider the following phase diagram that describes the one-dimensional motion of an object of mass m.
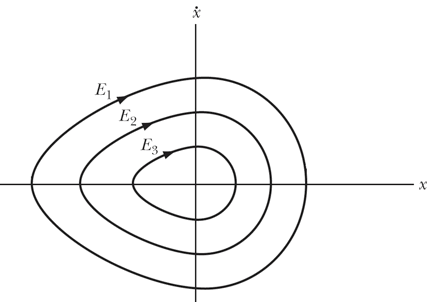
For this phase diagram answer the following questions:
1. What is the location of the equilibrium position? You need to motivate your answer!
2. Is the equilibrium a stable or an unstable equilibrium? You need to motivate your answer!
3. Rank the three energies, E1, E2, and E3, from largest to smallest.
Sketch the potential associated with the phase diagram. In particular, pay attention to the symmetry of the potential around the equilibrium position.
Your answers must be well motivated.
PROBLEM 7 (CONTINUED) ANSWER IN BOOK 3
b) Consider the following phase diagram that describes the one-dimensional motion of an object of mass m.
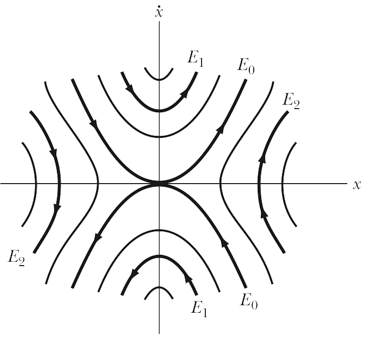
For this phase diagram answer the following questions:
1. What is the location of the equilibrium position? You need to motivate your answer!
2. Is the equilibrium a stable or an unstable equilibrium? You need to motivate your answer!
3. Rank the three energies, E0, E1, and E2, from largest to smallest.
Sketch the potential associated with the phase diagram. In particular, pay attention to the symmetry of the potential around the equilibrium position.
Your answers must be well motivated.
PROBLEM 7 (CONTINUED) ANSWER IN BOOK 3
c) Consider the following phase diagram that describes the motion of a plane pendulum of mass m and length l.
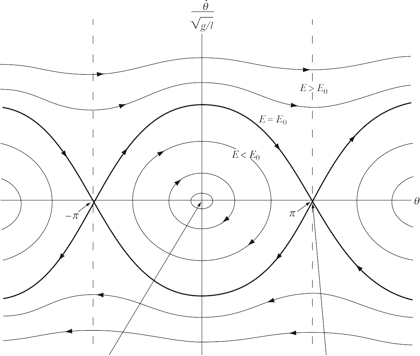
Derive the expression for the phase path of the plane pendulum (angular velocity as function of angle) if the total energy E exceeds E0 = 2mgl.
Your answers must be well motivated.
PROBLEM 8 (15 POINTS) ANSWER IN BOOK 3
A plumb line is often used to define the vertical direction on the surface of the Earth. According to Merriam-Webster dictionary, the definition of a plumb line is: “a line (as of cord) that has at one end a weight (such as a plumb bob) and is used especially to determine verticality.” If the Earth would be a good inertial reference frame, the plumb line would be along the direction of the gravitational acceleration, which is indeed the vertical direction with respect to the surface of the Earth.
Consider we use a plumb line in our laboratory to define the vertical direction. Our laboratory is located on the Northern hemisphere at an angle of latitude l. The Earth is rotating around its North-South axis, and the angular velocity w associated with this rotation is pointing North.
a) What is the angle between the plumb line and the true vertical direction?
b) What is the direction of the displacement of the plumb line (North, East, South, or West)?
Your answers must be well motivated and expressed in terms of the variables provided.
PROBLEM 9 (5 POINTS) ANSWER IN BOOK 3
Describe what happens on pakjes avond.
