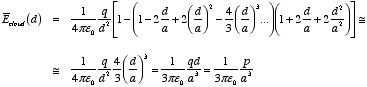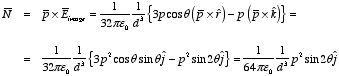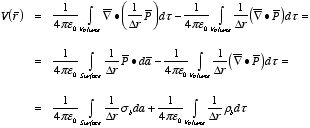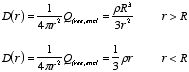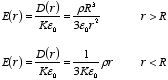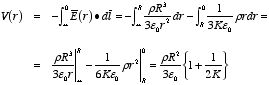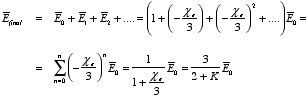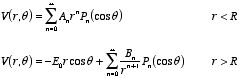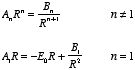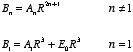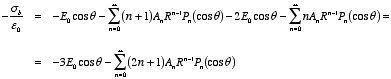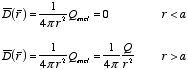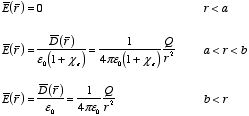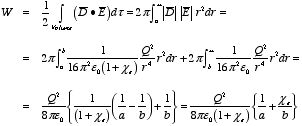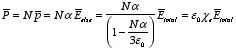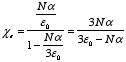Chapter 4. Electrostatic Fields in Matter
4.1. Polarization
A neutral atom, placed in an external electric field, will experience no
net force. However, even though the atom as a whole is neutral, the positive
charge is concentrated in the nucleus (radius = 10-14 m) while the
negative charge forms an electron cloud (radius = 10-10 m)
surrounding the nucleus (see Figure 4.1). The nucleus of the atom will
experience a force pointing in the same direction as the external electric field
(to the right in Figure 4.1) and of magnitude qEext. The
negatively charged electron cloud will experience a force of the same magnitude,
but pointed in a direction opposite to the direction of the electric field. As
a result of the external force, the nucleus will move in the direction of the
electric field until the external force on it is canceled by the force exerted
on the nucleus by the electron cloud.
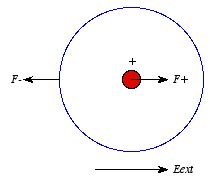 Figure
4.1. Atom in external electric field.
Figure
4.1. Atom in external electric field. Consider an electron cloud with a constant volume charge density
ρ and a radius a. If the total charge of the electron cloud
is -q then the corresponding charge density ρ is equal
to
The electric field inside the uniformly charged cloud is equal to
where r is the distance from the center of the cloud. Suppose that
as a result of the external electric field the nucleus moves by a distance
d with respect to the center of the electron cloud. The electric force
exerted on the nucleus by the electron cloud is equal to
The equilibrium position of the nucleus is that position where the external
force is canceled by the force exerted on it by the electron cloud:
This expression can be rewritten as
The equilibrium distance d is thus equal to
The induced dipole moment
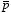
of the atom is defined as
Therefore, the magnitude of the induced dipole moment is proportional to
the magnitude of the external electric field, and its direction is equal to the
direction of the external electric field. The constant of proportionality is
called the atomic polarizability α and is defined
as
Although this model of the atom is extremely crude, it produces results
that are in reasonable agreement with direct measurements of the atomic
polarizability.
Example: Problem 4.2
According to quantum
mechanics, the electron cloud for a hydrogen atom in its ground state has a
charge density equal to
where q is the charge of the electron and a is the Bohr
radius. Find the atomic polarizability of such an atom.
As a result of
an external electric field the nucleus of the atom will be displaced by a
distance d with respect to the center of the electron cloud. The force
exerted on the nucleus by the electron cloud is equal to
where

is the electric field generated by the electron cloud. The electric field
generated by the electron cloud can be calculated using Gauss's law:
The displacement of the nucleus will be very small compared to the size of
the electron cloud (d«a). Therefore, we can expand
exp(-2d/a) in terms of d/a:
The nucleus will be in an equilibrium position when the electric force
exerted on it by the external field is equal to the electric force exerted on it
by the electron cloud. This occurs when the electric field at the position of
the nucleus, generated by he electron cloud, is equal in magnitude to the
externally applied electric field, but pointing in the opposite direction. The
dipole moment of the dipole can therefore be expressed in terms of the external
field:
The electric polarizability of the material is therefore equal to
which is close to the result obtained using the classical model of the
atom.
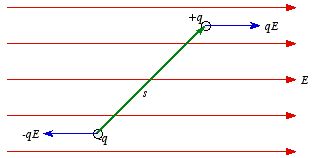 Figure
4.2. Torque on dipole in an electric field.
Figure
4.2. Torque on dipole in an electric field. Besides polarizing the atoms of a material, the external electric field can
align its molecules. Some molecules, like water, have a permanent dipole
moment. Normally, the dipole moments of the water molecules will be directed
randomly, and the average dipole moment is zero. When the water is exposed to
an external electric field, a torque is exerted on the water molecule, and it
will try to align its dipole moment with the external electric field. This is
schematically illustrated in Figure 4.2. Figure 4.2 shows a dipole
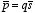
placed in an electric field, directed along the
x axis. The net force on
the dipole is zero since the net charge is equal to zero. The torque on the
dipole with respect to its center is equal to
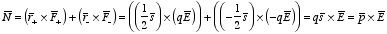
As a result of this torque, the dipole will try to align itself with the
electric field. When the dipole moment is pointing in the same direction as the
electric field the torque on the dipole will be equal to
zero.
Example: Problem 4.6 A dipole with dipole moment
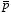
is situated a distance
d above an infinite grounded conducting plane (see
Figure 4.3). The dipole makes and angle
θ with the perpendicular to
the plane. Find the torque on
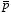
.
If the dipole is free to rotate, in what direction will it come to
rest?
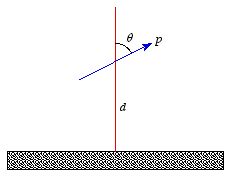 Figure
4.3. Problem
4.6
Figure
4.3. Problem
4.6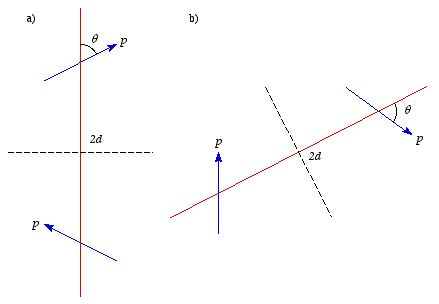 Figure
4.4. Method of images (Problem 4.6).
Figure
4.4. Method of images (Problem 4.6). This problem can be solved using the method of images (see Figure 4.4a).
Note that the method of images, when applied to a dipole, does not produce an
exact mirror image of the dipole. After defining the image dipole, we chose a
new coordinate system such that the image dipole is located at the origin, and
pointing upwards (along the positive z axis, see Figure 4.4b). The
electric field at the position of the real dipole due to the image dipole is
equal to
The torque on the real dipole is equal to
The torque on the dipole is positive when 0 < θ <
π/2 and as a consequence the dipole will rotate counter clockwise
towards the stable orientation of θ = 0. The torque on the dipole
is negative when π/2 < θ < π and as a
consequence the dipole will rotate clockwise towards the stable orientation of
θ = π.
Example: Problem 4.7
Show
that the energy of a dipole in an electric field is given by
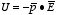
 Figure
4.5. Problem 4.7.
Figure
4.5. Problem 4.7. Consider the dipole located at the origin of a coordinate system. The
z axis of the coordinate system coincides with the direction of the
electric field and the angle between the dipole and the z axis is equal
to θ (see Figure 4.5). The energy of the system can be determined
by calculating the work to be done to move the dipole from infinity to its
present location. Assume the dipole is initially oriented parallel to the
x axis and is first moved from infinity along the x axis to
r = 0. The force exerted on the dipole by the electric field is directed
perpendicular to the displacement and therefore the work done by this force is
equal to zero. The dipole is then rotated to its final position (from
π/2 to θ). The torque exerted by the electric field on
the dipole is equal to
In order to rotate the dipole I must supply a torque opposite to
:
Therefore, the work done by me is equal to
The potential energy of the dipole is therefore equal to
and reaches a minimum when
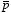
is parallel to
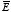
(the dipole is aligned with the electric field).
4.2. The Field of a Polarized Object
Consider a piece of polarized material with a dipole moment per unit
volume equal to
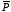
.
The electrostatic potential generated by this material is equal to
where
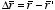
.
Using the following relation (one of the product rules of the vector
operator)
we can rewrite the expression for the electric potential as
where
and
Here the unit vector
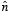
is perpendicular to the integration surface (and pointing outwards). The
equation for the electrostatic potential shows that the potential (and therefore
also the electric field) generated by a polarized object is equal to the
potential generated by an object with surface charge density
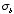
and volume charge density
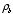
.
Example:
Problem 4.10 A sphere of radius
R carries a
polarization
where
k is a constant and
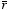
is the vector from the center.
a) Calculate the bound charges
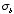
and
.
b) Find
the field inside and outside the sphere.
a) The unit vector
on the surface of the sphere is equal to the radial unit vector. The bound
surface charge is equal to
The bound volume charge is equal to
b) First consider the region outside the sphere. The electric field in
this region due to the surface charge is equal to
The electric field in this region due to the volume charge is equal
to
Therefore, the total electric field outside the sphere is equal to
zero.
Now consider the region inside the sphere. The electric field in this
region due to the surface charge is equal to zero. The electric field due to
the volume charge is equal to
The bound charges introduced in this Section are not just mathematical
artifacts, but are real charges, bound to the individual dipoles of the
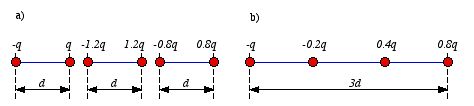
material. Consider for example the three dipoles shown in Figure 4.6a. When
they are aligned (lengthwise) the center charges cancel, and the system looks
like a single dipole with dipole moment 3dq (see Figure 4.6b).
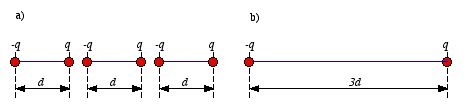 Figure
4.6. Aligned dipoles.
Figure
4.6. Aligned dipoles. In a uniformly polarized material of thickness
s and polarization
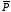
all dipoles are perfectly aligned (see Figure 4.7). The net result of the
alignment of the individual dipoles is a positive surface charge on one side of
the material and negative surface charge on the opposite side. Consider a
cylinder with surface area
A whose axis is aligned with the direction of
polarization of the polarized material. The total dipole moment of this
cylinder is equal to
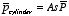
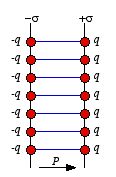 Figure.
4.7. Uniform polarization.
Figure.
4.7. Uniform polarization.Since the only charge of the system resides on the end caps of the cylinder
(volume charges cancel in a uniformly polarized material: see Figure 4.6), the
net charge there must be equal to
The charge density on the surface is therefore equal to
If the surface of the material is not perpendicular to the direction of
polarization then surface charge density will be less than P (surface
charge distributed over a larger area) and equal to
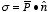
where
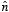
is the unit vector perpendicular to the surface of the material, pointing
outwards. For the material shown in Figure 4.7 this equation immediately shows
that a positive surface charge resides on the right surface
(
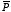
parallel to
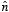
)
and a negative surface charge resides on the left surface
(
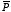
anti parallel to
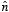
).
Since these charges reside on the surface and are bound to the dipoles they are
called the
bound surface charge or
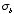
.
If
the material is uniformly polarized then the volume charge density is equal to
zero (see Figure 4.6). However, if the polarization is not uniform then there
will be a net volume charge inside the material. Consider a system of three
aligned dipoles (see Figure 4.8). If the polarization is not uniform then the
strength of the individual dipoles will vary. Assuming that the physical size
(length) of the dipoles shown in Figure 4.8 is the same, then the varying dipole
strength is a result of variations in the charge on the ends of the dipoles.
Since the net charge on the polarized material must be equal to zero, the sum of
the volume charges and surface charges must be equal to zero. Thus
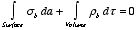
This equation can be rewritten by substituting the expression for the
surface charge density and applying the fundamental theorem of
divergences:
Since this relation holds for any volume we can conclude that
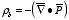
 Figure
4.8. Non-uniform polarization.
Figure
4.8. Non-uniform polarization. Example: Problem 4.31 A dielectric cube of side
s,
centered at the origin, carries a "frozen-in" polarization
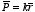
,
where
k is a constant. Find all the bound charges, and check that they
add up to zero.
The bound volume charge density
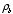
is equal to
Since the bound volume charge density is constant, the total bound volume
charge in the cube is equal to product of the charge density and the
volume:
The surface charge density
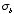
is equal to
The scalar product between
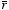
and
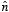
can be evaluate easily (see Figure 4.9) and is equal to
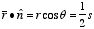
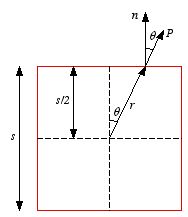 Figure
4.9. Problem 4.31.
Figure
4.9. Problem 4.31.Therefore the surface charge density is equal to
The surface charge density is constant across the surface of the cube and
consequently the total surface charge on the cube is equal to the product of the
surface charge density and the total surface area of the cube:
The total bound charge on the cube is equal to
4.3. The Electric Displacement
The electric field generated by a polarized material is equal to the
electric field produced by its bound charges. If free charges are also present
then the total electric field produced by this system is equal to the vector sum
of the electric fields produced by the bound charges and by the free charges.
Gauss's law can also be used for this type of systems to calculate the electric
field as long as we include both free and bound charges:
where
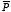
is the polarization of the material. This expression can be rewritten
as
The expression in parenthesis is called the
electric displacement
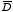
which is defined as
In terms of
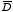
,
Gauss's law can be rewritten as
and
These two versions of Gauss's law are particularly useful since they make
reference only to free charges, which are the charges we can
control.
Although it seems that the displacement
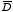
has properties similar to the electric field
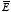
there are some very significant differences. For example, the curl of
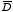
is equal to
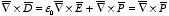
and is in general not equal to zero. Since the curl of
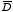
is not necessarily equal to zero, there is in general no potential that
generates
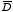
.
The
Helmholtz theorem tell us that if we know the curl and the divergence of a
vector function
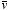
then this is sufficient information to uniquely define the vector function
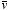
.
Therefore, the electric field
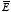
is uniquely defined by Gauss's law since we know that he curl of
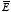
is zero, everywhere. The displacement current
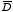
on the other hand is not uniquely determined by the free charge distribution,
but requires additional information (like for example
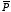
).
Example:
Problem 4.16 Suppose the field inside a large piece of dielectric is
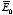
,
so that the electric displacement is equal to
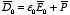
.
a) Now,
a small spherical cavity is hollowed out of the material. Find the field at the
center of the cavity in terms of
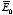
and
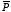
.
Also find the displacement at the center of the cavity in terms of
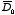
and
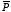
.
b) Do
the same for a long needle-shaped cavity running parallel to
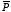
.
c) Do
the same for a thin wafer-shaped cavity perpendicular to
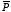
.
a) Consider
a large piece of dielectric material with polarization
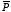
and a small sphere with polarization
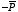
superimposed on it. The field generated by this system is equal to the field
generated by the dielectric material with a small spherical cavity hollowed out
(principle of superposition). The electric field inside a sphere with
polarization
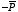
is uniform and equal to
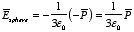
(see Example 2 of Griffiths). The field at the center of the cavity is
therefore equal to
The corresponding electric displacement at the center of the cavity is
equal to
b) Consider a large piece of dielectric material with polarization
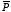
and a small long needle-shaped piece with polarization
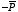
superimposed on it. The field generated by this system is equal to the field
generated by the dielectric material with a small long needle-shaped cavity
hollowed out (principle of superposition). The electric field of a polarized
needle of length
s is equal to that of two point charges (+
q and
-
q) located a distance
s apart. The charge on top of the needle
will be negative, while the charge on the bottom of the needle will be positive.
The charge density on the end caps of the needle is equal to
P.
Therefore,
where A is the surface area of the end caps of the needle. The
electric field generated by the needle at its center is equal to
In the needle limit
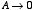
and therefore
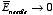
.
Thus at the center of the needle cavity
The electric displacement at this point is equal to
c) Consider a large piece of dielectric material with polarization
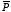
and a thin wafer-shaped piece of dielectric material with polarization
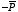
superimposed on it. The field generated by this system is equal to the field
generated by the dielectric material with a thin wafer-shaped cavity hollowed
out (principle of superposition). The electric field inside the wafer will be
that of two parallel plates with charge densities equal to -
σ on the
top and +
σ on the bottom. For a thin wafer-shaped cavity the
electric field between the plates will be equal to the field of a parallel-plate
capacitor with infinitely large plates. Thus
The net electric field in the center of the cavity is therefore equal
to
The electric displacement at the center of the cavity is equal to
4.4. Linear Dielectrics
Most dielectric materials become polarized when they are placed in an
external electric field. In many materials the polarization is proportional to
the electric field:
where
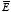
is the
total electric field (external + internal). The constant
of proportionality,
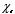
,
is called the
electric susceptibility. Materials in which the induced
polarization is proportional to the electric field are called
linear
dielectrics.
The electric displacement in a linear dielectric is also
proportional to the total electric field:
where ε is called the permittivity of the material which
is equal to
The constant
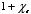
is called the
dielectric constant K of the material.
Consider
a volume
V entirely filled with linear dielectric material with
dielectric constant
K. The polarization
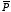
of this material is equal to
and is therefore proportional to
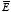
everywhere. Therefore
and consequently
The electric displacement
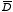
therefore satisfies the following two conditions:
and
The electric field generated by the free charges when the dielectric is not
present satisfies the following two equations:
and
Comparing the two sets of differential equations for
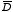
and
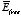
we conclude that
The displacement
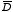
can also be expressed in terms of the total field inside the
dielectric:
These two equations show that
The presence of the dielectric material therefore reduces the electric
field by a factor
K.
Example: Problem 4.18 The space
between the plates of a parallel-plate capacitor (see Figure 4.10) is filled
with two slabs of linear dielectric material. Each slab has thickness
s,
so that the total distance between the plates is 2
s. Slab 1 has a
dielectric constant of 2, and slab 2 has a dielectric constant of 1.5. The free
charge density on the top plate is
σ and on the bottom plate is
-
σ.
a) Find the electric displacement
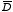
in each slab.
b) Find the electric field
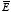
in each slab.
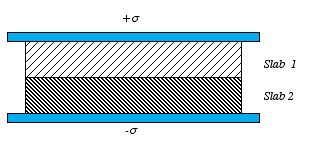
c) Find the polarization
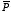
in each slab.
d) Find the potential difference between the plates.
e) Find
the location and amount of all bound charge.
f) Now that you know all charges
(free and bound), recalculate the field in each slab, and compare with your
answers to b).
 Figure
4.10. Problem 4.18.
Figure
4.10. Problem 4.18.a) The electric displacement
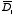
in slab 1 can be calculated using "Gauss's law". Consider a cylinder with cross
sectional area
A and axis parallel to the
z axis, being used as a
Gaussian surface. The top of he cylinder is located inside the top metal plate
(where the electric displacement is zero) and the bottom of the cylinder is
located inside the dielectric of slab 1. The electric displacement is directed
parallel to the
z axis and pointed downwards. Therefore, the
displacement flux through this surface is equal to
The free charge enclosed by this surface is equal to
Combining these two equations we obtain
In vector notation
In the same way we obtained for slab 2
b) The electric field
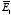
in slab 1 is equal to
The electric field
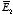
in slab 2 is equal to
c) Once
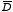
and
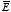
are known, the polarization
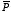
can be calculated:
Therefore, the polarization of slab 1 is equal to
The polarization of slab 2 is equal to
d) The potential difference between the top plate and the bottom plate is
equal to
e) There are no bound volume charges (constant polarization). The bound
surface charge density on the surface of a dielectric with polarization
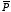
is equal to
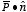
.
For slab 1 the polarization is equal to
The surface charge density on the top of slab 1 is equal to
The surface charge density on the bottom of slab 1 is equal to
For slab 2 the polarization is equal to
The surface charge density on the top of slab 2 is equal to
The surface charge density on the bottom of slab 2 is equal to
f) The total charge above slab 1 is equal to σ -
σ/2 = σ/2. This charge will produce an electric field
in slab 1 equal to
The total charge below slab 1 is equal to σ/2 - σ/3
+ σ/3 - σ = - σ/2. This charge will produce
an electric field in slab 1 equal to
The total electric field in slab 1 is the vector sum of these two fields
and is equal to
The total charge above slab 2 is equal to σ - σ/2 +
σ/2 - σ/3 = 2σ/3. This charge will produce
an electric field in slab 2 equal to
The total charge below slab 1 is equal to σ/3 - σ =
- 2σ/3. This charge will produce an electric field in slab 1 equal
to
The total electric field in slab 1 is the vector sum of these two fields
and is equal to
These answers are in agreement with the results obtained in part
b).
Example: Problem 4.20 A sphere of linear dielectric
material has embedded in it a uniform free charge density
ρ. Find
the potential at the center of the sphere, if its radius is
R and its
dielectric constant is
K.
The system has spherical symmetry and
therefore the electric displacement
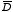
is easy to calculate since
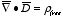
and
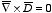
.
The calculation of
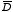
is very similar to the calculation of
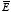
using Gauss's law:
The corresponding electric field is equal to
Here we have used the fact that K = 1 in the region outside the
sphere (r > R). The potential at the center of the sphere can
be calculated using this electric field:
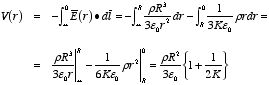
The examples of calculations involving polarized material that have
been discussed so far are either artificial, in the sense that the polarization
is specified at the start, or highly symmetric, so that the electric
displacement can be obtained directly from the free charge. In the next couple
of examples we will encounter systems where these special conditions do not
apply.
Example: Example 7 (Griffiths) and Problem 4.23 A
sphere of linear dielectric material (dielectric constant
K) is placed in
an originally uniform electric field
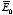
(note: we will assume that this electric field is directed along the positive
z axis).
a) Find the new field inside the sphere.
b) Solve for
the field inside the sphere by the method of separation of variables. Note
that: (1)
V is continuous at
R; (2) the discontinuity in the
normal derivative of
V at the surface is equal to
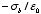
;
(3) because the dielectric is linear
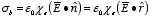
.
a) Suppose
the electric field inside the sphere is equal to
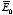
.
Since the material is a linear dielectric the polarization is proportional to
the total electric field:
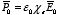
However, a uniformly polarized sphere with polarization
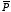
produces an internal electric field equal to
The electric field produced by the polarization of the sphere will
therefore reduce the electric field inside the sphere by
This change in the electric field will change the polarization of the
sphere by
This change in the polarization of the sphere will again change the
electric field inside the sphere. This change of the electric field strength is
equal to
This iterative process will continue indefinitely, and the final electric
field will be equal to
The final polarization of the sphere is therefore equal to
b) Since the dielectric will be uniformly polarized, all the bound charge
will reside on the surface of the sphere:
Therefore, the charge density is zero everywhere except on the surface of
the sphere. The electrostatic potential of this system must therefore satisfy
Laplace's equation (see Chapter 3). The most general solution of Laplace's
equation for this system is
Note that the potential does not approach zero when
r approaches
infinity since the electric field at infinity is equal to
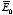
.
The electrostatic potential has to be continuous at
r =
R.
Thus
This relation requires that
These two equations can be rewritten as
The normal derivative of V at the surface of the sphere must satisfy
the following boundary condition:
Note that since the sphere is neutral, there is no free charge present.
Therefore, the total surface charge on the sphere is equal to the bound surface
charge. Substituting the general solution for V in this equation we
obtain
This equation can be rewritten by using the expressions for
Bn in terms of An with the following
result:
The bound charge is determined by the electric field, and therefore by the
gradient of the potential:
Combining the last two equations we obtain
This equation shows that for n = 1:
and for n ≠ 1:
These two equations can be rewritten as
and for n ≠ 1
The electrostatic potential since the sphere is thus equal to
We conclude that the electrostatic potential inside the sphere only depends
on the z coordinate. The electric field inside the sphere can be
obtained from the gradient of the electrostatic potential:
which is identical to the result we obtained in a).
Example:
Problem 4.35 Prove the following uniqueness theorem: A region
S
contains a specified free charge distribution
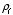
and various pieces of linear dielectric material, with the susceptibility of
each one given. If the potential is specified on the boundary of
S (and
V = 0 at infinity) then the potential throughout
S is uniquely
defined.
Suppose that there are two different solutions
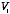
and
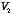
.
The corresponding electric fields are
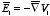
and
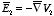
,
respectively. The corresponding electric displacements are
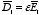
and
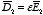
.
Consider a third function
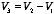
.
Since
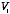
and
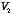
must have the same value on the border,
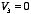
there. Now consider the volume integral (over volume
S) of
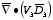
:
since
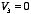
on the surface of volume
S. The left-hand side of this equation can be
rewritten as
But the divergence of
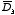
is equal to zero since
Therefore
The integral on the right-hand side of this equation can be rewritten in
terms of
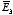
using the following relations:
and
Therefore,
Since
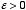
this equation can only be satisfied if
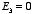
.
This requires that
and
everywhere. We therefore conclude that there are no two different
electrostatic potentials that satisfy the same boundary conditions. The
electrostatic potential is therefore uniquely defined if its value is specified
on the surface of the volume
S.
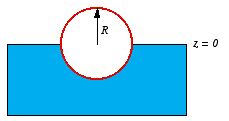
Example: Problem
4.36 A conducting sphere at potential
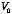
is half embedded in linear dielectric material of susceptibility
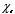
,
which occupies the region
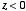
(see Figure 4.11).
Claim: the potential everywhere is exactly the same
as it would have been in the absence of the dielectric! Check this claim as
follows:
a) Write down the formula for the suggested potential
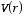
,
in terms of
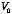
,
R, and
r. Use it to determine the field, the polarization, the
bound charge, and the free charge distribution on the sphere.
b) Show that
the total charge configuration would indeed produce the potential
.
c) Appeal
to the uniqueness theorem in Problem 4.35 to complete the argument.
 Figure
4.11. Problem 4.36.
Figure
4.11. Problem 4.36.a) In the absence of the dielectric, the electrostatic potential of this
system is constant inside the sphere and is given by
in the region outside the sphere. The electric field in the region outside
the sphere is equal to the gradient of V and is therefore given
by
If this solution satisfies the boundary conditions on the surface of the
sphere when the dielectric is present then it is the only solution (uniqueness
theorem of problem 4.35). The boundary conditions for the electrostatic
potential are:
1. V is continuous on the surface of the sphere.
This boundary condition is satisfied by the proposed solution.
2. The
difference in the normal derivative of V on the surface of the sphere is
equal to
For the proposed solution this requires that
which shows that the total charge is uniformly distributed across the
surface of the sphere.
The polarization of the dielectric material in
the region z < 0 (and r > R) can be obtained from the
electric field:
In the region z > 0 the polarization is equal to zero since no
dielectric material is present there. The bound surface charge on the surface
of the dielectric is equal to
where
is the surface vector (perpendicular to the surface and pointing out of the
dielectric). For the spherical surface
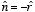
and thus
There is no bound charge on the flat surface (
z = 0) of the
dielectric since
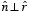
is there. The bound volume charge is zero everywhere since
The free charge on the surface of the sphere can be determined from the
electric displacement
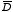
.
The electric displacement
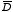
can be obtained from the electric field. In the region above the dielectric
(
z > 0) and outside the sphere (
r >
R) the electric
displacement
is equal to
In the region
z < 0 and outside the sphere (
r >
R) the electric displacement
is equal to
The free charge on the bottom hemisphere and part of the z = 0 plane
(see Figure 4.12a) is equal to
There is no contribution to the surface charge from the
z = 0 plane
since
there. The free charge density on the bottom hemisphere is therefore equal
to
In the same manner we can calculate the free charge density on the top
hemisphere:
The total charge density (bound charge + free charge) on the surface is
therefore equal to
Therefore, the total charge on the surface of the sphere is distributed
uniformly, and has a value consistent with the boundary condition for the normal
derivative of V. Since the proposed solution satisfies the boundary
conditions for V it will be the only correct solution.
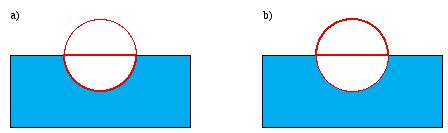 Figure
4.12. Determination of free charge in Problem 4.36.
Figure
4.12. Determination of free charge in Problem 4.36.
4.5. Energy in dielectric systems
Consider a capacitor with capacitance C and charged up to a
potential V. The total energy stored in the capacitor is equal to the
work done during the charging process:
If the capacitor is filled with a linear dielectric (dielectric constant
K) than the total capacitance will increase by a factor
K:
and consequently the energy stored in the capacitor (when held at a
constant potential) is increased by a factor
K. A general expression for
the energy of a capacitor with dielectric materials present can be found by
studying the charging process in detail. Consider a free charge
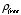
held at a potential
V. During the charging process the free charge is
increased by
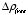
.
The work done on the extra free charge is equal to
Since the divergence of the electric displacement
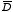
is equal to the free charge density
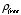
,
the divergence of
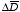
is equal to
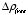
.
Therefore,
Using the following relation
we can rewrite the expression for ∆W as
The first term on the right-hand side of this equation can be rewritten
as
since the product of potential and electric displacement approach zero
faster than 1/r2 when r approached infinity.
Therefore,
Assuming that the materials present in the system are linear dielectrics
then
This relation can be used to rewrite
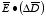
:
The expression for
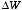
can thus be rewritten as
The total work done during the charging process is therefore equal
to
Note: this equation can be used to calculate the energy for a
system that contains linear dielectrics. If some materials in the system are
non-linear dielectrics than the derivation given above is not correct
(
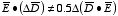
for non-linear dielectrics).
Example: Problem 4.26 A
spherical conductor, of radius
a, carries a charge
Q. It is
surrounded by linear dielectric material of susceptibility
χe, out to a radius
b. Find the energy of this
configuration.
Since the system has spherical symmetry the electric
displacement
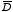
is completely determined by the free charge. It is equal to
Since we are dealing with linear dielectrics, the electric field
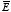
is equal to
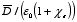
.
Taking into account that the susceptibility of vacuum is zero and the
susceptibility of a conductor is infinite we obtain for
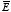
:
The scalar product
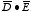
is equal to
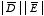
since
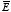
and
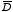
are parallel, everywhere. The energy of the system is equal to
4.6. Forces on dielectrics
A dielectric slab placed partly between the plates of a parallel-plate
capacitor will be pulled inside the capacitor. This force is a result of the
fringing fields around the edges of the parallel-plate capacitor (see Figure
4.13). Note: the field outside the capacitor can not be zero
since otherwise the line integral of the electric field around a closed loop,
partly inside the capacitor and partly outside the capacitor, would not be equal
to zero.
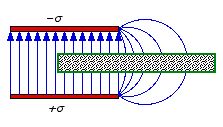 Figure
4.13. Fringing fields.
Figure
4.13. Fringing fields.Inside the capacitor the electric field is uniform. The electric force
exerted by the field on the positive bound charge of the dielectric is directed
upwards and is canceled by the electric force on the negative bound charge (see
Figure 4.14). Outside the capacitor the electric field is not uniform and the
electric force acting on the positive bound charge will not be canceled by the
electric force acting on the negative bound charge. For the system shown in
Figure 4.14 the vertical components of the two forces (outside the capacitor)
will cancel, but the horizontal components are pointing in the same direction
and therefore do not cancel. The result is a net force acting on the slab,
directed towards the center of the capacitor.
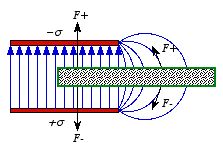 Figure
4.14. Forces on dielectric.
Figure
4.14. Forces on dielectric.A direct calculation of this force requires a knowledge of the fringing
fields of the capacitor which are often not well known and difficult to
calculate. An alternative method that can be used is to determine this force is
to calculate the change in the energy of the system when the dielectric is
displaced by a distance ds. The work to be done to pull the dielectric
out by an infinitesimal distance ds is equal to
where
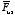
is the force provided by us to pull the slab out of the capacitor. This force
must just be equal in magnitude but directed in a direction opposite to the
force
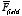
exerted by the electric field on the slab. Thus
The work done by us to move the slab must be equal to the change in the
energy of the capacitor (conservation of energy). Consider the situation shown
in Figure 4.15 where the slab of dielectric is inserted to a depth s in
the capacitor. The capacitance of this system is equal to
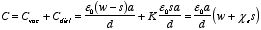
 Figure
4.15. Calculation of
Figure
4.15. Calculation of
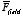 .
.If the total charge on the top plate is Q then the energy stored in
the capacitor is equal to
The force on the dielectric can now be calculated and is equal to
Example: Problem 4.28
Two long coaxial cylindrical metal
tubes (inner radius a, outer radius b) stand vertically in a tank
of dielectric oil (susceptibility χe, mass density
ρ). The inner one is maintained at potential V, and the
outer one is grounded. To what height h does the oil rise in the space
between the tubes?
The height of the oil is such that the electric force
on the oil balances the gravitational force. The capacitance of an empty
cylindrical capacitor of height H is equal to
If the oil rises to a height h then the capacitance of the capacitor
is equal to
The electric force on the dielectric (the oil) is equal to
and is directed upwards The gravitational force acting on the oil is equal
to
and is directed downwards. In the equilibrium position
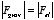
.
Thus
or
For a linear dielectric, the polarization
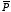
is proportional to the total macroscopic field

:
The polarization of the dielectric is equal to the vector sum of the
polarization
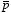
of the individual atoms or molecules:
where N is the number of atoms or molecules per unit volume. The
polarization of an individual atom or molecule is proportional to the
microscopic field at the position of the atom or molecule due to everything
except the particular atom or molecule under consideration:
The dipole moment of the atom or molecule will generate an electric field
at its center equal to
where R is the radius of the atom or molecule. The total
macroscopic field seen by the atom or molecule is there for equal to
where N is the number of atoms per unit volume. The total
polarization of the dielectric is thus equal to
Therefore
This equation can be rewritten in terms of the dielectric constants
K as
or
This equation shows that a measurement of the macroscopic parameter
K can be used to obtain information about the microscopic parameter
α. This equation is known as the Clausius-Mossotti formula
or the Lorentz-Lorenz equation.