Home Work Set # 7, Physics 217, Due: October 31,
2001
Problem 1
Find the potential outside an infinitely long metal pipe, of radius
R, placed at right angles to an otherwise uniform electric field
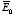
.
Find the surface charge induced on the pipe.
Problem 2
Find the potential outside a
charged metal sphere (charge
Q,
radius
R) placed in an otherwise uniform electric field
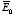
.
Explain clearly where you are setting the zero of the potential.
Problem 3
A long cylindrical shell of radius
R carries a uniform surface
charge
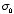
on the upper half, and an opposite surface charge
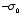
on the lower half (see Figure 1). Find the electric potential inside and
outside the cylinder.
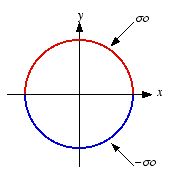 Figure
1. Problem 3.
Figure
1. Problem 3.
Problem 4
In Example 3.9 of Griffiths we derived the exact potential of a spherical
shell of radius
R which carries a surface charge
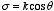
.
a) Calculate
the dipole moment of this charge distribution.
b) Find the approximate
potential, at points far from the sphere, and compare this with the exact answer
(eq. (3.87) of Griffiths). What can you conclude about the higher
multipoles?
Problem 5
A "pure" dipole p is situated at the origin, pointing in the
z direction.
a) What is the force on a point charge q at
(a, 0, 0) (Cartesian coordinates)?
b) What is the force on q at
(0, 0, a)?
c) How much work does it take to move q from
(a, 0, 0) to (0, 0, a)?
