Home Work Set # 4, Physics 217, Due: October 3,
2001
Problem 1
Find the electrostatic potential inside and outside a uniformly charged
solid sphere whose radius is R and whose total charge is q. Use
infinity as your reference point. Compare the gradient of V in each
region, and check that it yields the correct electric field.
Problem 2
Find the electrostatic potential a distance r from an infinitely
long straight wire that carries a uniform line charge λ. Compute
the gradient of your potential, and check that it yields the correct electric
field (calculated using Gauss's law).
Problem 3
A conical surface (an empty ice-cream cone) carries a uniform surface
charge σ. The height of the cone is a, as is the radius of
the bottom (see Figure 1). Find the potential difference between points
P (the vertex) and Q (the center of the bottom).
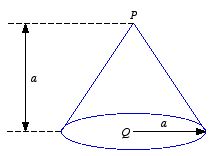 Figure
1. Problem 3.
Figure
1. Problem 3.
Problem 4
Find the potential on the axis of a uniformly charged solid cylinder, a
distance z from the center. The length of the cylinder is L, its
radius is R, and the charge density is ρ. Use your result to
calculate the electric field at this point. (Assume that z >
L/2.)
Problem 5
a) Three charges are situated at the corners of a square (side s) as
shown in Figure 2. How much work does it take to bring in another charge, +
q, from far away and place it at the fourth corner?
b) How much work
does it take to assemble the whole configuration of these four
charges?
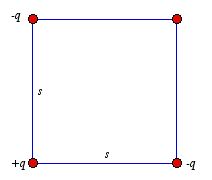 Figure
2. Problem 5.
Figure
2. Problem 5.
Problem 6
Find the energy stored in a uniformly charged solid sphere of radius
R and total charge q. Do it in three different ways:
a) Use
the following equation
and the electric field generated by a uniformly charged sphere.
b) Use
the following equation
and the electrostatic potential of a uniformly charged sphere.
c) Use
the following equation
and take as integration volume a sphere of radius
a. What happens
as
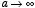
?
Problem 7
In this problem we will explore a fourth way of calculating the
electrostatic potential energy of the uniformly charged sphere of problem 6.
Assemble the sphere layer by layer, each time bringing in an infinitesimal
charge dq from far away and smearing it uniformly over the surface,
thereby increasing the radius. How much work dW does it take to build up
the radius by an amount dr? Integrate this to find the work necessary to
put together the entire sphere of radius R and total charge q.
Compare your answer with the results of Problem 6.


