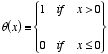Home Work Set # 2, Physics 217, Due: September 19,
2001
Problem 1
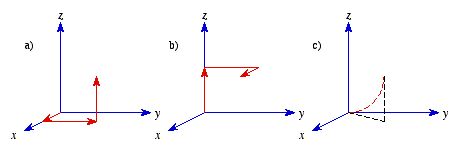
Check the fundamental theorem for gradients, using the function
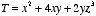
and the points
a = (0, 0, 0) and
b = (1, 1, 1), and the following
three paths (see Figure 1).
a) (0, 0, 0) → (1, 0, 0) → (1, 1, 0)
→ (1, 1, 1)
b) (0, 0, 0) → (0, 0, 1) → (0, 1, 1) →
(1, 1, 1)
c) The parabolic path
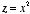
;
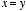
 Figure
1. Problem 1.
Figure
1. Problem 1.
Problem 2
Evaluate the following
integrals:
a)
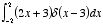
b)
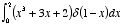
c)
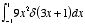
d)
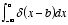
Problem 3
One consequence of the fundamental theorem for curls is that the surface
integral of the curl of a vector function
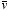
depends only on the boundary line, not on the particular surface used. Consider
the following vector function:
a) Calculate the line integral of
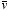
along the boundary of the square shown in Figure 2a.
b) Calculate the surface
integral of
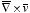
over the surface of the square shown in Figure 2a.
c) Calculate the surface
integral of
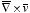
by integrating over the five sides of the cube shown in Figure 2b.
d) Compare
the result of part a) with the result of part b) and c). What do you
conclude?
 Figure
2. Problem 3.
Figure
2. Problem 3.
Problem 4
a) Show that
Hint: Use integration by parts.
b) Let
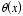
be the "step function":
Show that
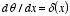
.
Problem 5
a) Let
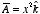
and
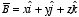
.
Calculate the divergence and curl of
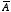
and
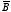
.
Which one can be written as the gradient of a scalar? Find a scalar potential
that does the job. Which one can be written as the curl of a vector function?
Find a suitable vector potential.
b) Show that
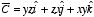
can be written both as the gradient of a scalar and as the curl of a vector.
Find scalar and vector potentials for this function.
Problem 6
a) Compute the divergence of the function
b) Check the divergence theorem for this function, using as you volume the
inverted hemisphere of radius R, resting on the x-y plane
and centered at the origin (see Figure 3).
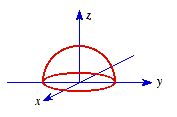 Figure
3. Problem 6.
Figure
3. Problem 6.
Problem 7
Compute the line integral of
along the triangular path shown in Figure 4. Check your answer using
Stokes' theorem.
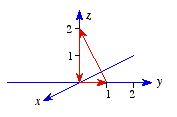 Figure
4. Problem 6.
Figure
4. Problem 6.