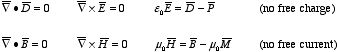Home Work Set # 11, Physics 217, Due: December 12,
2001
Problem 1
A coaxial cable consists of two very long cylindrical tubes, separated by
linear insulating material of magnetic susceptibility
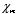
.
A current
I flows down the inner conductor and returns along the outer
one; in each case the current distributes itself uniformly over the surface (see
Figure 1). Find the magnetic field in the region between the tubes. As a
check, calculate the magnetization and bound currents and confirm that (together
of course with the free currents) they generate the correct field.
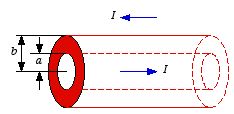 Figure
1. Problem 1.
Figure
1. Problem 1.
Problem 2
a) A current
I flows down a straight wire of radius
R. If
the wire is made of linear material (copper or aluminum) with susceptibility
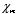
,
and the current is distributed uniformly, what is the magnetic field a distance
r from the center?
b) Find all the bound currents.
c) What is the
net bound current flowing down the wire?
Problem 3
Notice the following parallel:
Thus, the transcription
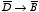
,
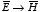
,
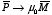
,
and
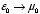
turns an electrostatic problem into an analogous magnetostatic one. Use this
observation, together with your knowledge of the electrostatic results, to
calculate
a) The magnetic field inside a uniformly magnetized
sphere.
b) The magnetic field inside a sphere of linear magnetic material in
an otherwise uniform magnetic field.
c) The average magnetic field over a
sphere, due to steady currents within the sphere.
Problem 4
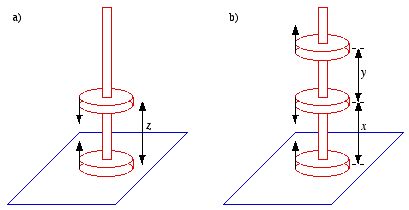
A familiar toy consists of donut-shaped permanent magnets (magnetization
parallel to the axis), which slide frictionless on a vertical rod (see Figure
2). Treat the magnets as dipoles, with mass
M and dipole moment
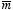
.
 Figure
2. Problem 4.
Figure
2. Problem 4.a) If you put two back-to-back magnets on the rod, the upper one will
"float" - the magnetic force upward balancing the gravitational force downward.
At what height z does it float?
b) If you now add a third magnet
(parallel to the bottom one), what is the ratio of the two heights? (Determine
the actual number, to three significant digits).
Problem 5
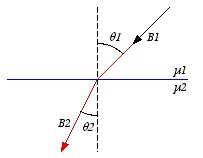
At the interface between one linear magnetic material and another magnetic
material the magnetic field lines bend (see Figure 3). Show that
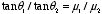
,
assuming there is no free current at the boundary.
 Figure
3. Problem 5.
Figure
3. Problem 5.