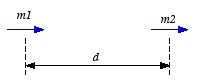Home Work Set # 10, Physics 217, Due: December 5,
2001
Problem 1
Find the force of attraction between two magnetic dipoles,
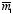
and
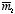
,
oriented as shown in Figure 1, a distance
d apart, using
(a) equation
(6.2) of Griffiths.
(b) equation (6.3) of Griffiths.
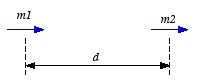 Figure
1. Problem 1.
Figure
1. Problem 1.
Problem 2
A uniform current density
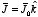
fills a slab straddling the
yz plane, from
x = -
a to
x = +
a. A magnetic dipole
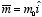
is situated at the origin.
a) Find the force on the dipole using equation
(6.3) of Griffiths.
b) Do the same for a dipole pointing in the
y-direction:
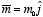
.
Problem 3
A long circular cylinder of radius
R carries a magnetization
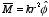
,
where
k is a constant,
r is the distance from the axis, and
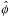
is the azimuthal unit vector. Find the magnetic field due to
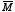
for points inside and outside the cylinder.
Problem 4
A short circular cylinder of radius
R and length
L carries a
"frozen-in" uniform magnetization
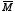
parallel to its axis. Find the bound current, and sketch the magnetic field of
the cylinder. (Make two sketches: one for
L >>
R, and one
for
L <<
R.)
Problem 5
Of the following materials, which would you expect to be paramagnetic and
which diamagnetic? Aluminum, copper, copper chloride (CuCl2),
carbon, lead, nitrogen (N2), salt (NaCl), sodium,
water.