1. Determine the angle between the body diagonals of a cube.

2. Prove the BAC-CAB rule (Griffiths, equation (1.17)) by writing out both sides in component form.

3. Find the transformation matrix R that describes a rotation by 120° about an axis from the origin through the point (1, 1, 1). The rotation is clockwise as you look down the axis toward the origin.

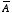
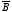
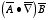
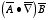
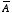
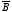
4. a) If and are two vector functions, what does the expression mean ? (That is, what are the x, y, and z components of in terms of the Cartesian components of , , and ?)
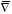
b) Suppose that

and

Check the following product rule by calculating each term separately:

5. The height of a certain hill (in feet) is given by

where y is the distance (in miles) north, and x is the distance east of South Hadley.
a) Where is the top of the hill located?
b) How high is the top of the hill?
c) How steep (in feet per mile) the hill at a point 1 mile north and 1 mile east of South Hadley? In what direction is the slope steepest, at that point?

6. a) Calculate the divergence of the following vector function:

b) Calculate the Laplacian of the following scalar function:

c) Calculate the Laplacian of the following vector function:

7. Show that

for a scalar function t and a vector function .
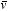