Midterm Exam # 2, Physics
217
November 28, 2001, 8.30 am – 9.50
am
Problem 1 (35 points)
A certain coaxial cable consists of
a copper wire, of radius a, surrounded by an infinitesimal thin
concentric copper tube of radius c (see Figure 1). The charge on the
wire is λ C/m and the charge on the tube is -λ C/m. The
space between the wire and the tube is partially filled (from b to
c) with a linear dielectric of susceptibility
χe.
a) What is the magnitude and direction of the
electric displacement in the three regions a < r < b,
b < r < c, and c < r?
b) What is
the magnitude and direction of the electric field in the three regions a
< r < b, b < r < c, and c
< r?
c) What is the capacitance per unit length of this
cable?
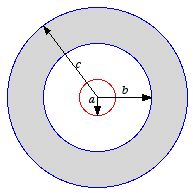 Figure
1. Problem 1.
Figure
1. Problem 1.
Problem 2 (35 points)
Consider a circular current loop of
radius R, lying in the xy plane, and carrying a current I
in the direction indicated (see Figure 2).
a) Find the exact magnetic field
(magnitude and direction) a distance z above the center of the current
loop.
b) What is the magnetic dipole moment of the current loop?
c) Verify
that for z » R the exact magnetic field calculated in a) is
consistent with the field of a magnetic dipole.
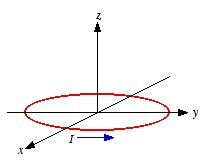 Figure
2. Problem 2.
Figure
2. Problem 2.
Problem 3 (35 points)
A uniform line charge λ
is placed on an infinite straight wire, a distance d above a grounded
conducting plane. The wire runs parallel to the x axis and directly
above it. The conducting plane is the xy plane.
a) Find the potential
in the region above the grounded plane.
b) Find the charge density
σ induced on the conducting plane.
Note: The potential
generated by a uniform line charge λ on an infinite straight wire is
equal to
where r is the distance from the line charge.


