Final Exam, Physics 217
December 20, 2001, 12.30 pm – 3.30
pm
1. Answer questions 1, 2, and 3 in exam book # 1.
Answer questions
4, 5, and 6 in exam book # 2.
2. Each question is worth 20 points: Yes,
your algebra is correct, and the total points you can score is 120 (a 20 point
bonus if you answer all 6 questions).
3. Each answer needs to be well
motivated. You will not receive any credit for just the answer (even if it is
correct) if no motivation is provided.
4. Here are some useful
relations:
The general solution of the following differential equation
is
where a is a constant.
5. The grades will be distributed via
email on or before 12/24.
6. Have a good and save holiday, and best
wishes for 2002.
7. All complaints/comments/questions about the exam and
the course should be directed to the instructor.
Problem 1 (20 points)
Find the force on the charge +q, shown in Figure 1, which is
located a distance of 3d above an infinitely large grounded conducting
plane, which is located in the xy plane.
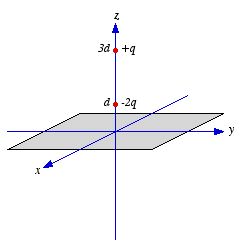 Figure
1. Problem 1.
Figure
1. Problem 1.Express your answer in terms of d and q. Make sure you
specify both the magnitude and the direction of the force.
Problem 2 (20 points)
Consider an infinitely long straight wire of radius
R, directed
along the
z axis, which carries a current
I.
a) What is the
magnetic field
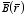
at a distance
r from the center of the wire (
r >
R)?
b) Find the vector potential
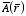
at a distance
r from the center of the wire (
r >
R).
c) Show that your solution in part b) is correct by verifying
that
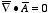
.
d) Show
that your solution in part b) is correct by verifying that
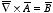
.
Express
all your answers in terms of
R,
I, and
r.
Problem 3 (20 points)
The electrostatic potential of some charge configuration is given by
the expression
where
A and
λ are constants.
a) Find the electric
field
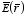
.
b) Find
the charge density
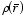
.
c) Find
the total charge
Q.
Express all your answers in terms of
A
and
λ.
Problem 4 (20 points)
A point charge q is imbedded at the center of a sphere of
linear dielectric material (with susceptibility χe and
radius R).
- Find the electric field
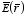 inside the sphere (r < R).
inside the sphere (r < R).
b) Find the
polarization
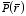
inside the sphere (
r <
R).
c) Find the bound volume and
surface charge densities
ρb and
σb.
d) What is the total bound surface charge on
the surface of the sphere?
e) Where is the opposing bound volume charge
located?
Express all your answers in terms of
q,
χe, and
R.
Problem 5 (20 points)
A certain transmission line in constructed from two thin metal
“ribbons” of width w, a very small distance h <<
w apart (see Figure 2). A current I travels down one strip and
back along the other. In each case, the current density across the ribbon is
uniform.
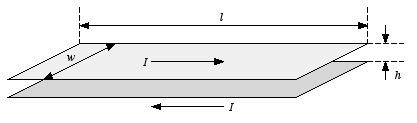 Figure
2. Problem 5.
Figure
2. Problem 5.
a) Find the capacitance per unit length C.
b) Find the
inductance per unit length L.
c) What is the product of C
and L?
d) If the strips are insulated from one another by a
non-conducting material of permittivity ε and permeability
μ, what will the product of C and L be?
Express
your answers in terms of h, w, ε, and
μ.
Problem 6 (20 points)
An infinitely long cylinder, of radius R, carries a "frozen-in"
magnetization, parallel to the axis,
where
k is a constant and
r is the distance from the axis
(there is no free current anywhere). Find the magnetic field inside and outside
the cylinder by two different methods:
a) Locate all the bound currents,
and calculate the field they produce.
b) Use Ampere's law to find
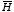
,
and then get
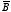
.
Express
you answers in terms of
k and
R.

