Problem 1 (2.5 points)

 

1

2

3

4

Match the above shown players of the best baseball team in the world with the following names:

 

            A.  Derek Jeter

            B.  Mariano Rivera

            C.  Johnny Damon

            D.  Jorge Posada

 

1234 =

a.     ABCD

b.     ACDB

c.     BADC

d.     BDAC

e.     CADB

f.      CABD

g.     DBAC

h.     DCBA

 

Problem 2 (2.5 points)

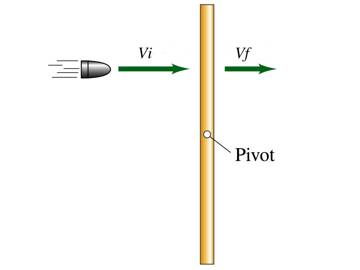
As you hold the string, a yoyo is released from rest so that gravity pulls it down, unwinding the string.  What is the angular acceleration of the yoyo, in terms of the string radius R, the moment of inertia I, and the mass M?

1.     g/(R + 2I/(MR))

2.     gMR/I

3.     gMR/(I + MR2)

4.     g/R

 

Problem 3 (2.5 points)

Suppose you are holding a bicycle wheel by a handle, connected to the axle, in front of you.  The axle points horizontally away from you and the wheel is spinning clockwise from your perspective.  You now try to tilt the axle to your left (center of mass moves leftward).  The wheel will swerve

1.     upward.

2.     downward.

3.     to your left.

4.     to your right.

 

Problem 4 (2.5 points)

An ideal gas is contained in a small volume, which is connected to a much larger volume that contains a vacuum.  Both volumes are insulated.  When the valve between the two volumes is opened, the gas will expand until it fills both volumes.  During this expansion, the gas

1.     does positive work.

2.     increases its internal energy.

3.     decreases its internal energy.

4.     does not change its internal energy.

 

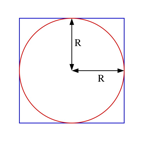AppleMark Problem 5 (2.5 points)

The moment of inertia of a square plate of area 4R2 and mass M, with respect to an axis through its center and perpendicular to the plate, is equal to (2/3)MR2.  A disk of radius R is removed from the center of the plate (see Figure).  What is the moment of inertia of the remaining material with respect to the same axis?

1.     (p/8)MR2

2.     (1/3 - p/12)MR2

3.     (1/6)MR2

4.     (2/3 - p/8)MR2

 

Problem 6 (2.5 points)

What is the heat capacity per atom or molecule in a solid

1.     3k

2.     3/2 k

3.     5/2 k

4.     7/2 k

 

Problem 7 (2.5 points)

What is the heat capacity at constant volume of a diatomic gas at a temperature T where kT is large compared to the energy of the first vibrational excited state?

1.     3k

2.     3/2 k

3.     5/2 k

4.     7/2 k

 

Problem 8 (2.5 points)

According to the Fundamental Assumption of Statistical Mechanics, which of the following states of an atom with three degrees of freedom and three quanta of energy is most probable?

1.     One degree of freedom with 3 quanta of energy and two degrees of freedom with 0 quanta of energy each.

2.     One degree of freedom with 2 quanta of energy, one degree of freedom with 1 quantum of energy, and one degree of freedom with 0 quanta of energy.

3.     Three degrees of freedom with 1 quantum of energy each.

4.     None of the above, because all microstates are equally probable.

 

Problem 9 (2.5 points)

Two wheels, initially at rest, roll the same distance without slipping down identical inclined planes.  Wheel B has twice the radius but the same mass as wheel A.  All the mass is concentrated in their rims, so that the rotational inertias are I = mR2.  Which wheel has the largest rotational kinetic energy when it gets to the bottom?

1.     Wheel A.

2.     Wheel B.

3.     The rotational kinetic energies are the same.

4.     Need more information.

 

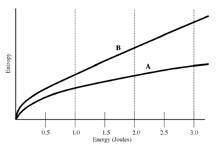Problem 10 (2.5 points)

The figure on the right shows a plot of the entropy of two different metal blocks as a function of the internal (thermal) energy.  Suppose the blocks (labeled A and B) are isolated from each other and are warmed until they each have 2 Joules of thermal energy.  Which block has a lower temperature at this energy?

1.     Block A has a lower temperature.

2.     Block B has a lower temperature.

3.     They have the same temperature since the thermal energy is the same.

4.     There is not enough information to determine the temperature.  The mass and specific heat of each block must be provided.

 

Problem 11 (25 points)

 

A cylinder with cross sectional area A contains N molecules of helium gas at pressure p0 and is in thermal equilibrium with a heat bath of temperature T0.  A piston confines the gas inside a region of volume V0.  The entire system is contained in a vacuum vessel, and only the helium gas exerts a pressure on the piston.  Assume that g = Cp/CV = 5/3 (for Helium).

 

a.     You quickly pull up the piston to increase the volume of the gas to Vf.  What is the temperature Tf of the gas immediately after you finish pulling up the piston?  What approximations did you make?

 

Since the piston is pulled up quickly we can assume that this is an adiabatic expansion.  During an adiabatic expansion p V g = constant.  Using the ideal gas law we can rewrite this in terms of the temperature T and the volume V: T V g-1 = constant.  Applying this relation to the expansion we conclude that

 

 

or

 

 

 

b.     What is the work done by the gas during this expansion?

 

The work done by the gas during the expansion can be found by determining the area under the p versus V curve:

 

 

 

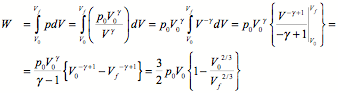
c.     What is the force you must exert on the piston, immediately after you finish pulling it up, in order to hold it into its final position?

 

Since pVg = constant we can easily calculate the pressure of the gas right after the adiabatic expansion:

 

 

The force on the piston is thus equal to

 

 

Note: we could have also used the ideal gas law and the temperature calculated in part a) to determine the final pressure:

 

 

d.     You wait until the helium returns back to its original temperature T0.  What is now the force you must exert on the piston in order to hold it into its final position?

 

We can use the ideal gas law to determine the pressure of the gas when it has returned to its original temperature T0:

 

 

The force on the piston at this point is thus equal to

 

 

e.     You now very slowly move the piston back to its original position such that the gas is contained in a volume V0.  How much work must you do to move the piston back to this position?  Is the magnitude of this work larger or smaller than the magnitude of the work calculated in part b?  What approximations did you make?

 

The compression we now carry out is an isothermal compression.  Since this compression is slow, there is ample of time to assure that the gas is maintained at a temperature T0.  The work done by the gas, which is opposite to the work that you need to do, can be calculated using the ideal gas law:

 

 

The work calculate in part b can be rewritten as

 

 

To compare the work done by these two processes, we really compare the work done during an isothermal process with the work done during an adiabatic process.  If we compare the area under the pV curve for an adiabatic process with the work done under the pV curve for an isothermal process with the same starting conditions (same p, same V) we see that the work done on the gas during an adiabatic compression is less than the work done by the gas during an isothermal expansion (see Figure below).

 

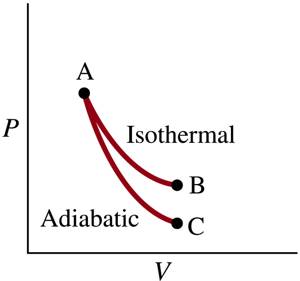
AppleMark

 

Problem 12 (25 points)

 

a.     What is the heat capacity per molecule at constant volume of a monatomic gas, such as helium or neon.  Why doesnÕt the heat capacity depend on temperature?

 

The heat capacity per molecule for a monatomic gas is 3/2k.  A monatomic gas only has 3 degrees of freedom (translational degrees of freedom) and no rotational or vibrational states that can be excited.  As a result, the number of degrees of freedom and thus the heat capacity is not temperature dependent.

 

b.     What is the heat capacity per molecule at constant volume of a diatomic gas, such as oxygen and nitrogen, at very high temperatures?

 

For a diatomic gas we need to consider the rotational and vibrational states.  At the highest temperature the total number of degrees of freedom is 7, and the heat capacity per molecule of the diatomic gas is 7/2k.

 

c.     Suppose we lower the temperature of a diatomic gas to a point where kT is small compared to the first excited rotational state.  What is the heat capacity per molecule at constant volume of this gas at this temperature?

 

When we lower the temperature to a point where kT is small compared to the first excited rotational state, the molecule will only have three degrees of freedom.  As a result, the heat capacity per molecule of the gas is 3/2k.

 

d.     The transition temperature Ttransition is the temperature at which the rotational properties of the gas molecules need to be taken into consideration when describing the properties of a gas.  Consider the following two gases: H2 (hydrogen, whose nuclei contain a single proton) and D2 (deuterium, whose nuclei contain a proton plus a neutron).  Estimate the ratio of the transition temperatures of these gases, Ttransition, hydrogen/Ttransition, deuterium.  Your answer needs to be well motivated and any approximations you have made must be clearly stated.

 

The energy of rotational states scale with 1/I, where I is the moment of inertia.  The lowest rotational state corresponds to a rotation around an axis that maximizes I.  The hydrogen and deuterium molecule have the same size (the molecular size is determined by the inter-atomic force which depends only on the electric force).  The largest moment of inertia is obtained when we consider a rotation around an axis perpendicular to the line connecting the two atoms.  The moment of inertia is proportional to the atomic mass, and the moment of inertia of deuterium is thus twice the moment of inertia of hydrogen: Ihydrogen /Ideuterium = 1/2.  The ratio of energies of the lowest rotational excited states is equal to DErot,hydrogen/DErot,deuterium = 2.  Since the energy of the molecules is proportional to T, we expect that the ratio of transition temperatures scales as the ratio of energies: Ttransition, hydrogen/Ttransition, deuterium = 2.

 

e.     Consider two volumes of hydrogen and deuterium gas, both maintained at the same temperature T.  The temperature T is low enough to ensure that the rotational and vibrational states are not excited.  Estimate the ratio of the speed of sound in hydrogen and deuterium gas, vsound, hydrogen/vsound, deuterium.  Your answer needs to be well motivated and any approximations you have made must be clearly stated.

 

The speed of sound is proportional to the root-mean-square speed of the molecules in the gas.  The rms speed of a gas molecule is equal to Ã(3kT/M).  Since both gases are maintained at the same temperature, their speed of sounds will differ due to differences in their molecular mass.  Since the mass of a deuterium molecule is twice the mass of a hydrogen molecule, the rms speed of the deuterium molecules will be 1/Ã2 times the rms speed of the hydrogen molecules.  The speed of sound in deuterium gas will thus be 1/Ã2 times the speed of sound in hydrogen gas: vsound, hydrogen/vsound, deuterium = Ã2.

 

Problem 13 (25 points)

 

A uniform stick of length H and mass M, initially at rest, is pivoted at its center.  A bullet of mass m is shot through the stick, midway between its pivot and one end (see Figure).

 

 

The bullet approaches the stick with a velocity vi and leaves with a velocity vf = (1/2)vi.  You can ignore the change in the mass and the moment of inertia of the rod as a result of the bullet passing through it.  You can also ignore the effect of gravity.

 

a.     What is the initial angular momentum of the bullet with respect to the pivot point?  Specify both its magnitude and its direction.

 

The arm of the initial linear momentum is H/4.  The magnitude of the initial angular momentum is equal to

 

 

Using the right-hand rule we can determine that the angular momentum is directed into the paper.

 

b.     What is the final angular momentum of the bullet with respect to the pivot point?  Specify both its magnitude and its direction.

 

The arm of the final linear momentum is H/4.  The magnitude of the initial angular momentum is equal to

 

 

Using the right-hand rule we can determine that the angular momentum is directed into the paper.

 

c.     With what angular speed is the stick spinning after the collision?

 

If we consider the bullet and the stick together, the collision force is an internal force and there are no external forces acting on the system.  The external torque is thus equal to zero, and angular momentum will be conserved.  Since the stick is initially at rest, its initial angular momentum will be equal to 0 kg m2/s.  Using conservation of angular momentum we can determine the angular momentum of the stick after the collision:

 

 

The moment of inertia of the stick is equal to (1/12)MH2.  The angular speed of the stick after the collision is thus equal to

 

 

d.     How much energy is lost in the collision?

 

The initial kinetic energy of the system is just the kinetic energy of the bullet.  It is equal to

 

 

The final kinetic energy is the sum of the kinetic energy of the bullet and the kinetic energy of the rotating rod.  The former is equal to

 

 

The final kinetic energy of the stick is equal to

 

 

The final kinetic energy is thus equal to

 

 

We immediately see that the final kinetic energy is less than the initial kinetic energy as long as (3/4)(m/M) < 3 or m < 4 M.  The energy that is lost in the interaction is equal to