Which of the diagrams in the following Figure corresponds to a system of two electrons that start out far apart, moving straight toward each other with nonzero initial velocities?
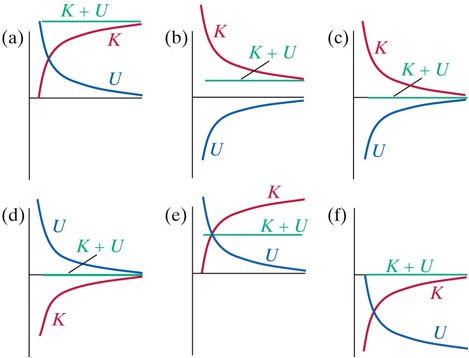
1.
(a)
2. (b)
3. (c)
4. (d)
5. (e)
6. (f)
Problem 2 (2.5 points)
One of the thermonuclear or fusion reactions that take place inside a star such as our Sun is the production of 3He and a high-energy photon in a collision between a proton (1H) and a deuteron (2H, the nuclear us ÒheavyÓ hydrogen, consisting of a proton and a neutron):
The rest mass of a proton is 1.0073 u (where u is the unified mass unit), the rest mass of the deuteron is 2.0136 u, the rest mass of 3He is 3.0155 u, and the mass of a photon is 0 u.
Which of the potential energy curves in the following Figure is a reasonable representation of the interaction in this fusion reaction?
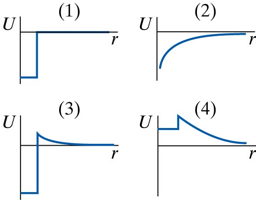
1. (1)
2. (2)
3. (3)
4. (4)
Problem 3 (2.5 points)
The Figure below shows a graph of the potential energy versus the interatomic distance for a particular molecule.
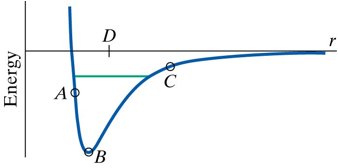
Rank the magnitude of the force at locations A, B, and C in order from strongest to weakest.
1. 
2. 
3.
4.
5.
6. 
Problem 4 (2.5 points)
What is so important about the number 42? Note that more than one answer may be correct.
1. That is the number that follows 41.
2. That is the number that precedes 43.
3. That is the number of points I hope to get on this exam.
4. That is the number of Mariano Rivera,
the last person who was able to use this number.
5. That is the number that was retired in
1997 to honor Jackie Robinson.
6. That is the number of airplanes your Physics 141 instructor owns.
Problem 5 (2.5 points)
Which energy diagram in the following Figure is appropriate for the following situations?
a)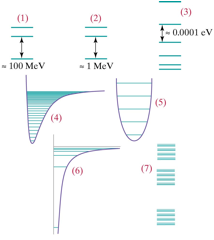 
Hadronic.
b) Vibrational states of a diatomic molecule such as O2.
c) Idealized quantized spring-mass oscillator.
d) Nuclear.
e) Vibrational and rotational states of a diatomic molecule such as O2.
f) Rotational states of a diatomic molecule such as O2.
g) Electronic states of a single atom such as hydrogen.
1. (1=a), (2=c), (3=d), (4=e), (5=g), (6=f), (7=b)
2. (1=a), (2=d), (3=f), (4=b), (5=c),
(6=g), (7=e)
3. (1=b), (2=a), (3=f), (4=d), (5=c), (6=g), (7=e)
4. (1=b), (2=a), (3=c), (4=g), (5=d), (6=f), (7=e)
5. (1=c), (2=d), (3=a), (4=b), (5=e), (6=f), (7=g)
6. (1=c), (2=d), (3=a), (4=g), (5=f), (6=e), (7=b)
7. (1=d), (2=a), (3=f), (4=b), (5=c), (6=g), (7=e)
8. (1=d), (2=b), (3=f), (4=a), (5=c), (6=g), (7=e)
Problem 6 (2.5 points)
You are given two carts, A and B. They look identical, and you are told that they are made of the same material. You place A at rest on an air track and give B a constant velocity directed to the right so that it collides elastically with A. After the collision, both carts move to the right, the velocity of B being smaller than what it was before the collision. What do you conclude?
1. Cart A
is hollow.
2. The two carts are identical.
3. Cart B is hollow.
4. Need more information.
Problem 7 (2.5 points)
A string is wrapped around a disk of mass M and radius R. Starting from rest, you pull the string with a constant force F along a nearly frictionless surface. At the instant when the center of the disk has moved a distance d, a length L has unwound of the disk. At this instant what is the speed of the center of mass of the disk?
1. 
2.
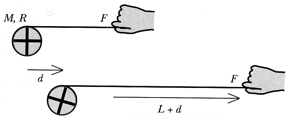
3.
4.
5.
Problem 8 (2.5 points)
If all
three collisions in the figure shown below are totally inelastic, which
collisions cause(s) the most damage?
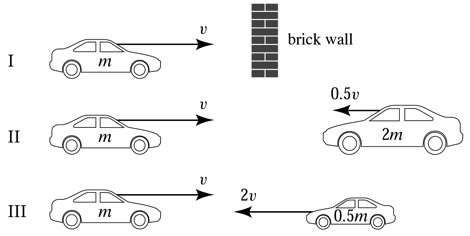
1. I.
2. II.
3. III.
4. I and II.
5. I and III.
6. II and III.
7. All three.
Problem 9 (2.5 points)
An energy diagram of the hydrogen atom with several transitions is shown in the Figure below.
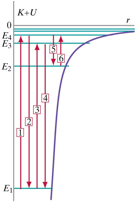
Assuming that the hydrogen is maintained at extremely low temperatures, which transition shown in the Figure represents an absorption transition that is extremely unlikely to be observed?
1. Transition 1
2. Transition 2
3. Transition 3
4. Transition 4
5. Transition 5
6.
Transition
6
Problem 10 (2.5 points)
Consider a head-on collision between two objects. Object 1, which has mass m1, is initially in motion and collides head-on with object 2, which has mass m2 and is initially at rest. Which of the following statements about the collision are true?
A.
B.
C.
If 
,
then 
.
D.
If 
,
then the final speed of object 2 is less than the initial speed of object 1.
E.
If 
,
then the final speed of object 1 is greater than the final speed of object 2.
1. A
2. A B
3. A B C
4. A B D
5. A B E
6. A C
7. A C D
8. A C E
9. A D
10. A E
Problem 11 (25 points)
A chain of metal links is coiled up in a tight ball on a frictionless table. The mass of the chain is m. You pull on a link at one end of the chain with a constant force F. Eventually the chain straightens out to its full length L, and you keep pulling until you have pulled your end of the chain a total distance d.
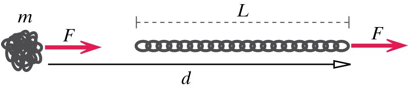
a. What is the speed of the chain at this instant?
Answer:
During the motion depicted in the Figure, the center of mass moves a
distance d - L/2. The work done by
the force on the center of mass during this motion is (d - L/2)F.
Since the initial kinetic energy of the center of mass is 0, the final
kinetic energy can be found by using the work-energy theorem
The final velocity of the center of mass is thus equal to
b. When the chain straightens out, the links of the chain bang against each other, and their temperature rises. Calculate the increase in thermal energy of the chain, assuming that the process is so fast that there is insufficient time for the chain to lose much thermal energy to the table.
Answer:
The total work done by the force F
is Fd. Part of the work is converted into
kinetic energy of the center of mass (see part a). The remainder is converted into thermal
energy of the chain (note there is no relative motion with respect to the
center of mass after the chain has been unrolled). The thermal energy is thus equal to the
difference between Fd and the work on
the center of mass calculated in part a:
Express all your answers in terms of the variables provided. Your answers must be well motivated.
Problem 12 (25 points)
Consider an inelastic collision in which a truck of mass M and a car of mass m collide in an icy intersection and stick together, as shown in the Figure below.
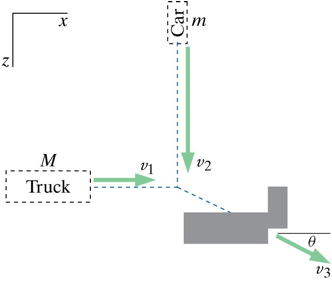
a) Let v1 be the initial speed of the truck, v2 the initial speed of the car, and v3 the final speed of the car and the truck when they are stuck together. What are the final speed v3 and the angle q between the direction of the car and truck after the collision and the x axis?
Answer:
The final velocity of the car and truck can be determined by applying
conservation of linear momentum in the x
and z directions. Using the information contained in the
Figure we see that
or
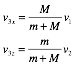
The speed of the car and truck after the collision can now be
determined:
The angle between the direction of the car and truck and the x axis can be obtained from the x and z components of the velocity of the system:
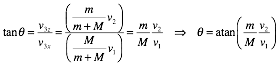
b) How much energy is lost in this collision?
Answer
The change in the kinetic energy in this collision is equal to
Using the velocity v3
calculated in part a we can now determine the change in the kinetic
energy. It is equal to
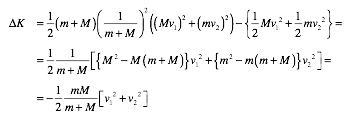
c) What is the velocity of the center of mass before the collision (specify both the direction and the magnitude or the x and z components of the center-of-mass velocity)?
Answer
The motion of the center of mass is not changed as a result of the
collision. After the collision, the
car and truck are stuck together and their velocity is equal to the velocity of
the center of mass, before and after the collision. Thus:
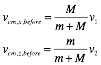
d) What is the velocity of the center of mass after the collision (specify both the direction and the magnitude or the x and z components of the center-of-mass velocity)?
Answer
The motion of the center of mass is not changed as a result of the
collision. After the collision, the
car and truck are stuck together and their velocity is equal to the velocity of
the center of mass, before and after the collision. Thus:
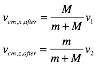
Express all your answers in terms of the variables
provided. Your answers must be well
motivated.
Problem 13 (25 points)
The cable of an
elevator of mass M snaps when the
elevator is a rest at one of the floors of a skyscraper. At this point the elevator is a distance d above a cushioning spring with spring
constant k. A safety device clamps the elevator
against the guide rails so that a constant frictional force f opposes the motion of the elevator. Find the maximum distance by which the
cushioning spring will be compressed.
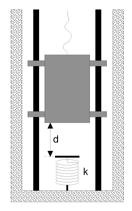
Answer:
We will take the top of the spring (in its rest position) to be the
position where the potential energy is equal to 0 J. When the elevator is at rest a distance d above the spring, it will only have
potential energy (E = mgd). When the cable snaps, the elevator will
move down, but its downward motion is slowed down by the clamps on the guide
rails that provide a constant frictional force f. The work done by the
friction force up to the point that the elevator reaches the spring is –fd.
The mechanical energy of the system at this point will thus be equal to mgd – fd. At this position,
all the mechanical energy is in the form of kinetic energy of the elevator.
Consider what happens when the spring is compressed by a distance x.
Assuming that this is the maximum compression (that is, the elevator has
come to rest), we know that the total mechanical energy of the system is
–mgx + (1/2)kx2. During the compression, the work done by
the friction force is –fx, and
the total mechanical energy must therefore also be equal to mgd – fd – fx. We thus require that
This equation can be rewritten as
which can be solved for x:
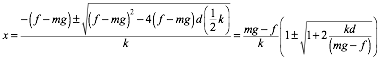
We should note that only the positive solution of x should be considered.
Express all your answers in terms of the variables provided. Your answers must be well motivated.