Two blocks of mass m1 and m3, connected by a rod of mass m2, are sitting on a frictionless surface. You push to the left on the right block with a constant force F.
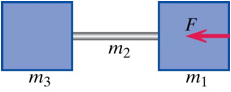
What is the compression force in the rod near its right end?
1. m1F/(m1 + m2 + m3)
2. m2F/(m1 + m2 + m3)
3. m3F/(m1 + m2 + m3)
4. (m1 + m2)F/m1
5. (m1 + m3)F/m2
6. (m2 + m3)F/m3
7. (m1 + m2)F/(m1 + m2 + m3)
8. (m1 + m3)F/(m1 + m2 + m3)
9.
(m2 + m3)F/(m1 + m2 + m3)
Problem 2 (2.5 points)
The z-component of the linear momentum of a ball is observed to
change with time in the following way:
At t = 0 s, pz = 12 kg m/s
At t = 1 s, pz = 7 kg m/s
At t = 2 s, pz = 2 kg m/s
At t = 3 s, pz = −3 kg m/s
Which of the following statements about the z component of the net force acting on the ball during the time the ball is
observed is true?
1. The z component of the net force on the ball
is zero.
2.
The z component of the net force on the ball
is constant.
3. The z component of the net force on the ball
is decreasing with time.
4. The z component of the net force on the ball
is increasing with time.
5.
Not enough information is given to determine the z component of the net force on the
ball.
Problem 3 (2.5 points)
A ball moves in the direction of the arrow labeled c in the Figure below.

The ball is truck by a stick that briefly
exerts a force on the ball in the direction of the arrow labeled e.
Which arrow best describes the direction of ![]() ,
the change in the ball’s linear momentum?
,
the change in the ball’s linear momentum?
1. a
2. b
3. c
4. d
5. e
6. f
7. g
8. h
9. j
Problem 4 (2.5 points)
Which fundamental interaction (gravitational, electromagnetic, strong, or weak) is responsible for each of the following processes:
a) A neutron outside a nucleus decays into a proton, electron, and antineutrino.
b) Protons and neutrons attract each other in a nucleus.
c) The Earth pulls on the Moon.
d) Protons in a nucleus repel each other.
1. (a) Gravitational, (b) Electromagnetic, (c) Strong, and (d) Weak.
2. (a) Electromagnetic, (b) Gravitational, (c) Strong, and (d) Weak.
3. (a) Gravitational, (b) Electromagnetic, (c) Weak, and (d) Strong.
4. (a) Strong, (b) Electromagnetic, (c) Gravitational, and (d) Weak.
5. (a) Electromagnetic, (b) Strong, (c) Gravitational, and (d) Weak.
6. (a) Weak, (b) Strong, (c) Gravitational,
and (d) Electromagnetic.
7. (a) Weak, (b) Electromagnetic, (c) Gravitational, and (d) Strong.
8. (a) Strong, (b) Weak, (c) Gravitational, and (d) Electromagnetic.
Problem 5 (2.5 points)
In the last 19 years, how many times did the Yankees miss the post season?
1.
 0 times.
0 times.
2. 1 time.
3. 2 times.
4. 3 times.
5. 4 times.
6. 5 times.
7. 6 times.
8. 12 times.
9. 19 times.
Problem 6 (2.5 points)
Which of the following statements is not correct?
1.
The momentum principle tells us that ![]() .
.
2. The principle of relativity states that physical laws work in the same way for observers in uniform motion as for observers at rest.
3. The momentum principle tells us that ![]() .
.
4. The velocity of an object is related to its momentum in the following manner
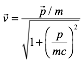
Problem 7 (2.5 points)
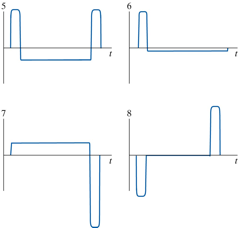
A cart rolls on a frictionless track. A fan is mounted on the cart, and when the fan is turned on, a constant force is acting on the cart. The fan is turned on and you hold the cart stationary. You then take your hand away and the cart moves forward, in the +x direction. After travelling a long distance along the track, you quickly stop and hold the cart.

a. The following four graphs display the x component of the net force acting on the cart as function of time. Which of these graphs matches the motion we just described?
PROBLEM CONTINUED ON NEXT PAGE
Problem 7 (continued)
b. The following four graphs display the position of the cart along the track as function of time. Which of these graphs matches the motion we just described?
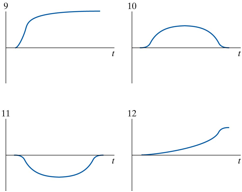
Select one of the answer combinations listed below.
1. Answer question a: Graph 5; Answer question b: Graph 9.
2. Answer question a: Graph 5; Answer question b: Graph 10.
3. Answer question a: Graph 5; Answer question b: Graph 12.
4. Answer question a: Graph 6; Answer question b: Graph 9.
5. Answer question a: Graph 6; Answer question b: Graph 10.
6. Answer question a: Graph 6; Answer question b: Graph 12.
7. Answer question a: Graph 7; Answer question b: Graph 9.
8. Answer question a: Graph 7; Answer
question b: Graph 12.
9. Answer question a: Graph 8; Answer question b: Graph 9.
10. Answer question a: Graph 8; Answer question b: Graph 10.
Problem 8 (2.5 points)
A box hangs motionless from two ropes, as shown in the Figure below.
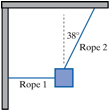
Which of the free-body diagrams shown in the Figure below correctly describes the forces acting on the box?
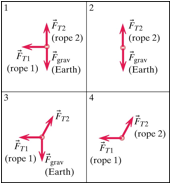
1. Diagram 1
2. Diagram 2
3. Diagram 3
4. Diagram 4
Problem 9 (2.5 points)
A comet orbits a star in an elliptical orbit, as shown in the Figure below. The linear momentum of the comet at location A is shown in the Figure.
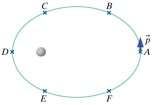
What is the direction of the change in the linear momentum of the comet when it is located at location C?
1. Direction a
2.
 Direction
b
Direction
b
3. Direction c
4. Direction d
5. Direction e
6. Direction f
7. Direction g
8. Direction h
9. Direction j
Problem
10 (2.5
points)
You have two identical springs. When you hang a mass m from one of the springs, the system oscillates with a period T.
Now you connect the two springs in parallel to mass m, as shown in the Figure below.

What will be the period of the mass now?
1. 4 T
2. 2 T
3. √2 T
4. T
5. T/√2
6. T/2
7. T/4
Problem 11 (25 points)
Consider the Earth to be a sphere of radius R and uniform density r. Suppose that a hole is drilled along the diameter of the Earth, straight through the center. After the hole is drilled, the air is pumped out of it.
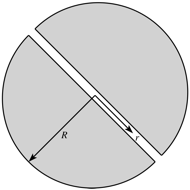
Consider a mass m dropped into the hole.
a. What is the magnitude of the net force exerted by the Earth on mass m when it is located a distance r from the center of the Earth? Take r < R.
Answer:
Based on
the shell theorem, only those segments of the Earth that are located closer
than a distance r from the center
will effect the force on mass m. Since the Earth is assumed to be
uniform, the mass that is responsible for the force on mass m is
![]()
The
shell theorem also tells use that the gravitational force on mass m due to the uniform sphere of radius r and mass M is identical to the gravitational force generated when all of
mass M is located at the center of
the Earth. The magnitude of the
force on mass m is thus equal to
![]()
b. What type of motion will result from this type of force?
Answer:
The
previous answer shows that the magnitude of the force on mass m is proportional to the displacement r.
Its direction is opposite to the direction of the displacement. These two conditions are required for
simple harmonic motion, which is the motion we expect for mass m.
c. How long will it take until mass m reaches the center of the Earth?
Answer:
Since
mass m will carry out simple-harmonic
motion, the time required to reach the center of the Earth will be 1/4th
of the period of the motion. The
force acting on the mass m was
determined in part a):
![]()
If we
compare this to the spring force, we see that the equivalent “spring constant” k will be
![]()
The
period T of the resulting
simple-harmonic motion is equal to
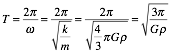
The time
to reach the center of the Earth is thus equal to
![]()
Express all your answers in terms of the variables provided. Your answers must be well motivated.
Problem 12 (25 points)
A ball of mass m is suspended from a string, and after given a push, moves along a horizontal circular path, as shown in the Figure below.
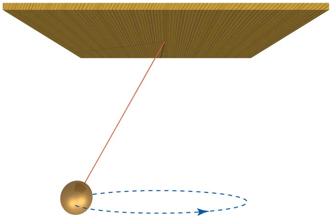
You measure the length of the string to be L and the angle between the string and the vertical axis to be q. You also time the motion and find that it takes T seconds for the ball to make one complete circular trip. From these measurements determine the gravitational constant g. You can ignore the mass of the string in your calculations.
Answer:
Based on
the length of the string and the angle between the string and the vertical
axis, we can determine the radius r
of the circular orbit:
![]() .
.
The
velocity of the ball can now be determined:
![]() .
.
In order
for the ball to carry out circular motion, the radial force acting on it must
have a magnitude of
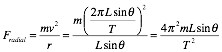 .
.
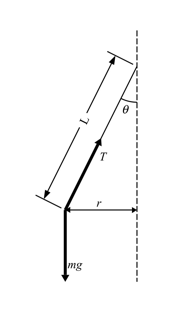 If we
look at the free-body diagram of the system, as shown in the Figure on the
right, we can determine the radial force based on the forces acting on the mass
(the tension T and the gravitational
force mg):
If we
look at the free-body diagram of the system, as shown in the Figure on the
right, we can determine the radial force based on the forces acting on the mass
(the tension T and the gravitational
force mg):
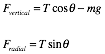
The net
vertical force on the mass must be 0 N.
This allows us to express the tension T in the string in terms of the gravitational force on the mass:
![]() .
.
The
radial force is thus equal to
![]() .
.
We now
have two expressions for the radial force:
![]() .
.
This
equation can be solved for g:
![]() .
.
Express all your answers in terms of the variables provided. Your answers must be well motivated.
Problem 13 (25 points)
In a cathode ray tube (CRT) used in older television sets, a beam of electrons is steered to different places on a phosphor screen, which glows at the locations hit by the electrons. The CRT is evacuated, so there are few gas molecules present for the electrons to run into. Electric forces are used to accelerate electrons of mass m to a speed v0, small compared to the speed of light, after which they pass between positively and negatively charged metal plates that deflect the electron in the vertical direction (upward in the Figure below, or downward if the sign on the charges on the plates is reversed).
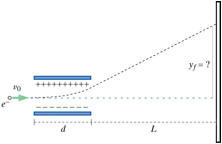
While the electron is between the plates, it experiences a uniform vertical force F, but when the electron is outside the plates, there is negligibly force acting on it. The gravitational force on the electron is negligible small compared to the electric force in this situation. The length of the metal plates is d, and the phosphor screen is a distance L from the metal plates. Where does the electron hit the screen? That is, what is yf?
Answer:
Approach
1:
The time
the electron spent between the plates is d/v0. The acceleration in the vertical
direction between the plates is F/m.
The vertical displacement of the electron during the time it is between
the plates is equal to
![]() .
.
When the
electron leaves the plate region, its horizontal velocity has not changed, but
its vertical velocity will be equal to
![]()
The
vertical displacement in the region beyond the plates can be found using the
ratio of the velocities:
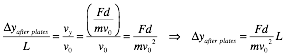
The
total displacement in the vertical direction is thus equal to
![]()
Approach
2:
Assume
that the length of the plates is small compared to the path length L and assume the vertical displacement
between the plates is small. The
time the electron spent between the plates is d/v0. The momentum principle can be used to
determine the change in the linear momentum in the vertical direction:
![]()
When the
electron leaves the plate region, its linear momentum in the x and y directions is equal to
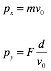
Using
these x and y components, we can determine yf:
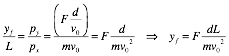
Express all your answers in terms of the variables provided. Your answers must be well motivated.